在leetcode上有一些系列的题目,题目比较类似,只是区别于有一些细节条件不同,难度也是从易到难不断升级,这类题目一个系列做下来,非常锻炼人的思维能力。
今天看看可以使用动态规划解决的买卖股票这个系列。
买卖股票的最佳时机(只能买卖一次)

对于每一天,有两种状态:
- 持有股票,可能是之前买的,也可能是当天买的。反正就是之前买过,但没有卖出。
- 不持有股票,可能之前就没买,或者已经卖了。
我们定义 dp[i][0] 表示第i天持有股票的收益, dp[i][1] 表示第i天未持有股票的收益。
对于持有股票而言,有可能是前一天持有股票,一直到今天。又或者是前一天未持有股票,当天买入的。
所以,对于持有股票的状态,会有 dp[i][0]=max(dp[i-1][0], -prices[i])。
这里为什么是-prices[i],而不是 dp[i-1][1]-prices[i]?
因为本题只允许买卖一次,既然是当天买的,那么前一天收益必然为0
对于未持有股票而言,有可能是前一天就未持有,一直到当天。也有可能是前一天持有股票,当天卖出的。
所以,对于未持有股票而言,状态为: dp[i][1]=max(dp[i-1][1], dp[i-1][0]+prices[i])。
所以最终的状态转移公式为:
1 | |-- dp[i][0]=max(dp[i-1][0], -prices[i]), 持有股票 |
1 | function maxProfit(prices: number[]): number { |
除了上面的状态定义方式,还可以根据买入卖出定义状态,即只买卖一次。是【买卖股票的最佳时机IV(最多买卖k次)】的一个特殊变种,k=1,只买卖一次。
具体思路及代码可参考【买卖股票的最佳时机IV(最多买卖k次)】
当然,除了动态规划,本题也可以使用贪心算法。
1 | function maxProfit(prices: number[]): number { |
买卖股票的最佳时机II(可以买卖多次)

本题是上面的升级,由只允许买卖一次变为允许买卖多次,但只允许持有一只股票。
状态定义和上题一模一样。只不过状态转移公式变一下。
由于可以允许买卖多次,因此,当第i天持有股票时,如果前一天未持有,则前一天的利润不再是0,而是 dp[i-1][1]。
1 | function maxProfit(prices: number[]): number { |
本题也可以用贪心算法。
由于可以买卖多次,我们只需要贪心的按股票价格的涨买即可,即在股票价格低点买,涨了后卖。
1 | function maxProfit(prices: number[]): number { |
买卖股票的最佳时机III(最多买卖两次)

本题又是一种变体。有原来的买卖不限次数变为限制买卖两次。
这样我们就不能再按上面的是否持有股票来定义状态了。
既然有限制买卖次数,那么我们就按买卖次数进行状态定义。
由于只能最多买卖两次,因此在每一天,我们有以下5种状态:
- 未进行任何买卖操作
- 只进行过一次买操作
- 进行过一次买和一次卖操作,即完成一次交易
- 完成一次交易后,又进行一次买操作
- 完成两次交易
对于第一种状态,未进行任何操作,收益为0,不做记录。
我们定义buy1,buy2,sell1,sell2为 收益状态,分别表示:
- buy1: 第一次买入后的 收益
- sell1: 第一次卖出后的 收益
- buy2: 第二次买入后的 收益
- sell2: 第二次卖出后的 收益
这样,我们针对每次的买卖,只需要取最大值即可。
对于买入,收益为 减去 当前价格。对于卖出,收益为 加上 当前价格。
状态转移公式: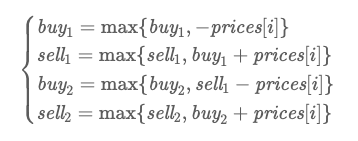
1 | |--buy1 = max(buy1, -prices[i]) |
最终我们只需要根据状态变化,计算状态即可。
1 | function maxProfit3(prices: number[]): number { |
买卖股票的最佳时机IV(最多买卖k次)

本题又是在最多买卖2次的基础上升级了,买卖次数限制为最多k次。
其思路也是一样,按照买卖次数进行状态定义。
我们定义 buys[i] 为第i次买入后的最大收益, sells[i] 为第i次卖出后的最大收益。
买入时,收益为上一次卖出后的收益减去当前价格。
卖出时,收益为本次买入后的收益加上当前价格。
那么,对应的状态转移方程是:
1 | buys[i] = max(buys[i], sells[i-1]-price) // 第i次买入后最大收益状态转移 |
实现代码:
1 | function maxProfit(k: number, prices: number[]): number { |
本题的k如果设置为1,就是上面【买卖股票的最佳时机(只能买卖一次)】的解。
本题的k如果设置为2,就是上面【买卖股票的最佳时机III(最多买卖两次)】的解。
对于【买卖股票的最佳时机(只能买卖一次)】可以借鉴【买卖股票的最佳时机III(最多买卖两次)】,定义状态时不需要定义数组,因为只买卖一次,因此只需要定义一个买入和卖出两个常量状态即可。
【买卖股票的最佳时机(只能买卖一次)】使用买卖次数定义状态的代码:
1 | function maxProfit(prices: number[]): number { |
买卖股票的最佳时机含手续费(买卖多次,每次有手续费)

本题是【买卖股票的最佳时机II(可以买卖多次)】的升级,可以买卖多次,但加了手续费,即每买卖一次需要交一次手续费。
状态定义和上面买卖股票II的一致。只不过,在每次卖出股票时,由于手续费的存在,在计算收益时需要减去手续费。
1 | function maxProfit(prices: number[], fee: number): number { |
买卖股票的最佳时机含冷冻期(买卖多次,卖出有一天的冷冻期)

本题又是【买卖股票的最佳时机II(可以买卖多次)】的升级,在其基础上加入了冷冻期概念。
这样我们买卖股票II定义的状态中,未持有股票这种状态会分裂出两种状态:1. 未持有股票,且处于冷冻期内 2. 未持有股票,但未处于冷冻期内。
这样,我们总共就有了三种状态:
- 持有股票
- 未持有股票,且处于冷冻期内
- 未持有股票,但未处于冷冻期内
我们定义
dp[i][0] 表示第i天持有股票时的最大收益,
dp[i][1] 表示第i天手上不持有股票,且处于冷冻期内的最大收益,
dp[i][2] 表示第i天不持有股票,但未处于冷冻期内的最大收益。
相应的,状态转移公式也会发生变化。
- 持有股票时,可能是前一天就持有,然后持有到当天。也可能是前一天不持有,当天买入的股票,那么前一天必然不持有股票,也未在冷冻期内。
dp[i][0] = max(dp[i-1][0], dp[i-1][2]-prices[i]) - 未持有股票,且处于冷冻期内。处于冷冻期内那么前一天必然持有股票且当天卖掉。此时的收益为前一天持有股票的最大收益加当天股票卖出的价格。
dp[i][1] = dp[i-1][0] + prices[i] - 未持有股票,但未处于冷冻期内。当天未处于冷冻期,前一天可能是处于冷冻期,也可能是未处于冷冻期。
dp[i][2] = max(dp[i-1][1], dp[i-1][2])
代码实现:
1 | function maxProfit(prices: number[]): number { |
总结
买卖股票这个系列的题,对条件不断的变种与延伸,可以说是动态规划算法很好的练习题目。
随着不断的升级与变种,加深对动态规划的理解,不同条件下如何定义状态,状态又是如何转移的,初始状态又该怎样定义等等。
即便是同一个题,在定义状态时也可以有不同的视角,可以说是非常不错的几个题目。