动态规划之爬楼梯

发表于   |   分类于 ，

爬楼梯是一个动态规划的入门题目，非常简单，也非常容易理解，一般将动态规划都是以爬楼梯作为例子来讲解。

虽然简单，但里面确有一些值得玩味的细节，今天来聊聊这个经典的爬楼梯。

爬楼梯

题目描述：

爬楼梯

1

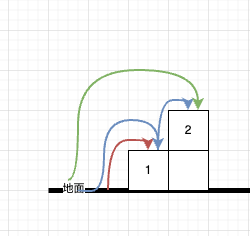
由于每次只能爬1个或2个台阶，因此，对于只有一个台阶的楼梯，只有一种方法，就是从地面爬1个台阶都楼顶（图中红色部分）。对于一个有2个台阶的楼梯而言，有2种方法，直接爬两个台阶到楼顶（图中绿色部分），或者每次一个台阶，爬两次到楼顶（图中蓝色部分）。

对于有n阶台阶的楼梯而言，有两种方式爬上来：

  1. 从n-1阶台阶，爬1个台阶上来
  2. 从n-2阶台阶，爬2个台阶上来

因此，我们定义 dp[i] 为爬i个台阶的方法数，则 dp[i] = dp[i-1]+dp[i-2]即为状态转移公式。

初始化状态，我们初始化 dp[0]=1, dp[1]=1。对于dp[1]=1很多人没有异议，但是对于dp[0]=1很多人不理解，dp[0]按定义就是爬0阶台阶的楼梯，应该等于0，怎么会等于1呢？

其实对于0阶台阶，即直接地面就是楼顶，本身也是一种方法，因此初始化时可以直接初始化为1。

1
2
3
4
5
6
7
8
9
10
function climbStairs(n: number): number {
  const dp = new Array(n + 1).fill(0);
  // 初始化状态
  dp[0] = 1, dp[1] = 1;
  for (let i=2;i<=n;i++) {
    dp[i] = dp[i-1]+dp[i-2];
  }

  return dp[n];
}

使用最小花费爬楼梯

爬楼梯

本题是上面 爬楼梯的升级，在爬的过程中需要支付相应的费用。

我们定义 dp[i] 表示爬到第i阶台阶所需要的最小花费。那么，爬到楼顶的最小花费即为 dp[length+1].

我们爬到第i阶台阶有两种方式：

  • 从i-1阶台阶，爬一个台阶上来
  • 从i-2阶台阶，爬2个台阶上来

由于我们可以选择从下标为0或者下标为1的台阶开始爬，因此会有 dp[0]=0，dp[1]=0。
即我们可以选择直接从地面爬，或者直接从第1阶台阶爬，这都是不需要费用的。

那么得到的状态转移公式便是 dp[i]=min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2])

1
2
3
4
5
6
7
8
function minCostClimbingStairs(cost: number[]): number {
  const dp = [0, 0];
  for (let i = 2; i <= cost.length; i++) {
    dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
  }

  return dp[cost.length]
};

爬楼梯进阶

我们做一下进阶，上面爬楼梯每次只能爬1个或2个台阶，但如果改一下，每次至多爬k个台阶呢？
对于一个有n阶台阶的楼梯，每次能爬1个，2个，3个，…，至多k个台阶，那么爬到楼顶有多少种方法？

k=2即是上面爬楼梯的题

如果每次只能爬1个或2个台阶，每次爬到第n个台阶时方法是固定的，就两种，从n-1阶台阶爬上来或从n-2阶台阶爬上来。

但是如果爬的方式不固定，可以1个，也可以2个，至多可以爬k个台阶，其实解决方法也是一样的。

对于爬n个台阶而言，我们可以从n-1爬上来，也可以从n-2爬上来，也可以从n-3爬上来，一直到可以从n-k爬上来。

我们只需要多加一层循环，来遍历爬楼梯的方式即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
function climbStairs(n: number, k: number): number {
  // 定义 dp[i] 为爬到第i个台阶时方法数
  const dp = new Array(n + 1).fill(0);
  dp[0] = 1, dp[1] = 1;

  for (let i = 2; i <= n; i++) {
    for (let j = 1; j <= k; j++) {
      if (i - j >= 0) {
        dp[i] = dp[i] + dp[i - j];
      }
    }
  }
  return dp[n];
}

代码中k=2即可当作上面普通爬楼梯题目的代码。