滑动窗口算法思想是非常重要的一种思想,可以用来解决数组,字符串的子元素问题。它可以将嵌套循环的问题,转换为单层循环问题,降低时间复杂度,提高效率。
滑动窗口的思想非常简单,它将子数组(子字符串)理解成一个滑动的窗口,然后将这个窗口在数组上滑动,在窗口滑动的过程中,左边会出一个元素,右边会进一个元素,然后只需要计算当前窗口内的元素值即可。
可用滑动窗口思想解决的问题,一般有如下特点:
- 窗口内元素是连续的。就是说,抽象出来的这个可滑动的窗口,在原数组或字符串上是连续的。
- 窗口只能由左向右滑动,不能逆过来滑动。就是说,窗口的左右边界,只能从左到右增加,不能减少,即使局部也不可以。
算法思路
- 使用双指针中的左右指针技巧,初始化 left = right = 0,把索引闭区间 [left, right] 称为一个「窗口」。
- 先不断地增加 right 指针扩大窗口 [left, right],直到窗口符合要求
- 停止增加 right,转而不断增加 left 指针缩小窗口 [left, right],直到窗口中的字符串不再符合要求。同时,每次增加 left,我们都要更新一轮结果。
- 重复第 2 和第 3 步,直到 right 到达尽头。
第 2 步相当于在寻找一个「可行解」,然后第 3 步在优化这个「可行解」,最终找到最优解。 左右指针轮流前进,窗口大小增增减减,窗口不断向右滑动。
代码模板
1 | left,right := 0,0 // 左右指针 |
注意:
- 滑动窗口适用的题目一般具有单调性
- 滑动窗口、双指针、单调队列和单调栈经常配合使用
滑动窗口的思路很简单,但在 leetcode 上关于滑动窗口的题目一般都是 mid 甚至 hard 的题目。其难点在于,如何抽象窗口内元素的操作,验证窗口是否符合要求的过程。
即上面步骤 2,步骤 3 的两个过程。
说的有点生涩。来两个例子说明一下。
连续子数组的最大和
给定一个整数数组,计算长度为 n 的连续子数组的最大和。
比如,给定 arr=[1,2,3,4],n=2,则其连续子数组的最大和为 7。其长度为 2 的连续子数组为[1,2],[2,3],[3,4],和最大就是 3+4=7。
所有问题都可以用穷举法解决,比如这个。我们可以穷举出所有长度为 n 的子数组,然后计算每个子数组的和,再求最大值。穷举法能实现,但是效率非常低。因为在穷举的过程中会嵌套循环。
滑动窗口的思想就是,把这个要求和的子数组当成一个窗口,然后在数组上滑动。如下图所示:
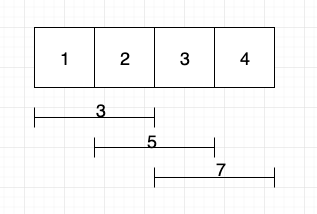
我们维护一个长度为 2 的窗口,然后依次滑动这个窗口直至结束。在滑动时,出一个左边元素,进一个右边元素,计算这个窗口内的元素和,然后和最大和比较。滑动结束,也就求出了最大和是多少。
1 | func maxSubSum(nums []int, n int) int { |
和为 target 的连续正整数序列
输入一个正整数 target ,输出所有和为 target 的连续正整数序列(至少含有两个数)。
序列内的数字由小到大排列,不同序列按照首个数字从小到大排列。
示例 1:
输入:target = 9
输出:[[2,3,4],[4,5]]示例 2:
输入:target = 15
输出:[[1,2,3,4,5],[4,5,6],[7,8]]限制:
1 <= target <= 10^5
这个题目初看上去,和滑动窗口没啥关系。上面说到了,滑动窗口一般解决的是数组或字符串,连续子元素相关的问题。这里没有数组啊?
虽然没有数组,但这里有一个很关键的点就是,输出要求是 连续正整数序列。这里的连续性是使用滑动窗口的关键点。
我们可以将从 1 到 target 这个整数序列,抽象成一个数组,然后使用滑动窗口思想,在这个序列上进行滑动求解。
对于滑动窗口思想,有一点需要记住:窗口只能从左到右,沿一个方向滑动。
1 | func findContinuousSequence(target int) [][]int { |
长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的连续子数组,并返回其长度。如果不存在符合条件的连续子数组,返回 0。
示例:
输入: s = 7, nums = [2,3,1,2,4,3]
输出: 2
解释: 子数组 [4,3] 是该条件下的长度最小的连续子数组。进阶:
如果你已经完成了 O(n) 时间复杂度的解法, 请尝试 O(n log n) 时间复杂度的解法。
这个问题可以说是上面一个题目的变形,上面一个是和正好等于 target,而这个是求和大于等于 target 的最小子序列长度。
上面这个题目窗口长度是固定的,这个是变长的。但其实利用滑动窗口的思想,难度也算简单。
和上面一个题目一样,我们只需要一个 sum 变量来存储窗口内元素的和即可。
当 sum<s 时,我们要增大窗口。此时,窗口右边界增加。
当 sum>=s 时,此时说明这个窗口是满足条件的,我们要判断此时窗口的长度是否是最小。另外,窗口左边界增加,缩小窗口。
不断重复增大,缩小窗口的操作,直至窗口到数组末尾。
1 | func minSubArrayLen(s int, nums []int) int { |
水果成篮
在一排树中,第 i 棵树产生 tree[i] 型的水果。
你可以从你选择的任何树开始,然后重复执行以下步骤:
- 把这棵树上的水果放进你的篮子里。如果你做不到,就停下来。
- 移动到当前树右侧的下一棵树。如果右边没有树,就停下来。
请注意,在选择一颗树后,你没有任何选择:你必须执行步骤 1,然后执行步骤 2,然后返回步骤 1,然后执行步骤 2,依此类推,直至停止。你有两个篮子,每个篮子可以携带任何数量的水果,但你希望每个篮子只携带一种类型的水果。
用这个程序你能收集的水果总量是多少?示例 1:
输入:[1,2,1]
输出:3
解释:我们可以收集 [1,2,1]。示例 2:
输入:[0,1,2,2]
输出:3
解释:我们可以收集 [1,2,2].
如果我们从第一棵树开始,我们将只能收集到 [0, 1]。示例 3:
输入:[1,2,3,2,2]
输出:4
解释:我们可以收集 [2,3,2,2].
如果我们从第一棵树开始,我们将只能收集到 [1, 2]。示例 4:
输入:[3,3,3,1,2,1,1,2,3,3,4]
输出:5
解释:我们可以收集 [1,2,1,1,2].
如果我们从第一棵树或第八棵树开始,我们将只能收集到 4 个水果。提示:
1 <= tree.length <= 40000
0 <= tree[i] < tree.length
这个题目,看完描述,都看不明白说的个啥。
其实这个题目很简单,就是说,给定的一个数组,表示果树上结的水果。数组中的每一个不同的值表示一种不同类型的水果。
现在你有两个篮子,需要从前往后收集水果。每个篮子只能装一种水果。收集的时候,需要注意,一个篮子只能装一种水果,且不能丢失重新装。
问最后你能最多装多少个水果。
再说直白点,这个题就是要你从一个整数数组中,找到其只包含两个元素的最长子数组。
理解了题意,这个题就很简单了。
我们定义一个滑动的窗口,表示收集水果的篮子。
如果窗口内收集的水果小于等于两种,那么我们增大窗口。
如果窗口内收集的水果多于两种,那么我们减小窗口。
然后在滑动的过程中,取到窗口的最大长度即可。
1 | func totalFruit(tree []int) int { |
最长不重复子串的长度
给定一个字符串 str,找出其中不含有重复字符的最长子串的长度。
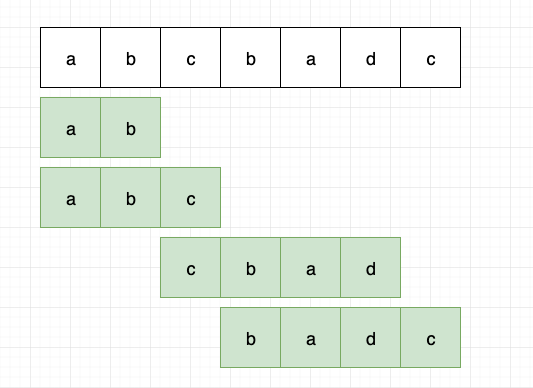
例如,str=”abcabcdd”,最长不重复子串”abcd”的长度为 4。
这个问题和上面一个一样,也是窗口长度不定,需要变长移动窗口。
不断增加窗口长度,如果在增加的过程中,遇到窗口中已经存在的字符,那么,将窗口左侧边界移动到当前已存在新入窗字符的位置。
1 | func lengthOfLongestSubstring(str string) int { |
字符串的排列
给定两个字符串 s1 和 s2,写一个函数来判断 s2 是否包含 s1 的排列。
换句话说,第一个字符串的排列之一是第二个字符串的子串。
示例 1:
输入: s1 = “ab” s2 = “eidbaooo”
输出: True
解释: s2 包含 s1 的排列之一 (“ba”).示例 2:
输入: s1= “ab” s2 = “eidboaoo”
输出: False注意:
输入的字符串只包含小写字母
两个字符串的长度都在 [1, 10,000] 之间
这个问题也可以用滑动窗口的思想来解决。因为我们在 s2 中判断子串是否是 s1 的排列时,这个子串在 s2 中一定是连续的。
我们抽象一个窗口,用于记录 s1 中每个字符应该出现的次数,然后把这个窗口放到 s2 上滑动判断。
当入窗时,次数减少。因为入窗相当于已经出现。
当出窗时,次数增加。出窗相当于入窗的逆操作。
1 | func checkInclusion(s1 string, s2 string) bool { |
最小覆盖子串
给定一个字符串 S,一个字符串 T,请在 S 中找出:包含 T 所有字母的最小子串。
示例:
输入:S=”ADOBECODEBANC”,T=”ABC”
输出:”BANC”
说明:
如果 S 中不存在这样的子串,返回空字符串””
如果 S 中存在这样的子串,我们保证它是唯一的答案。
定义两个变量 left,right,区间[left,right]表示窗口。
滑动窗口的 right 边界,直到窗口内已包含 T 中所有字符,此时停止 right 的滑动。
滑动窗口的 left 边界,直到窗口内不包含 T 中所有的字符,此时停止 left 的滑动。
继续上面两个步骤,直接窗口滑动到 S 的末尾。
滑动 left,right 边界简单。怎么判断窗口内是否包含 T 中所有字符呢?
我们可以使用和上面一样的方法。记录字符应该出现的次数。当 T 的所有字符,在窗口内的次数都大于 1 时,则说明窗口内已包含 T 的所有字符。
那么,怎么判断窗口内是否包含 T 中所有的字符呢?
我们可以使用出现次数来判断,如同上一个题一样。先将 T 中所有字符出现次数放入哈希表,表示窗口中各个字符应该出现的次数。
当窗口在滑动过程中,遇到 T 中的字符,那么说明这个字符已经出现,次数减一。当 T 中所有字符出现次数为 0 时,说明窗口内已经包含了 T 中所有的字符。
1 | func minWindow(s string, t string) string { |
滑动窗口最大值
给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
进阶:
你能在线性时间复杂度内解决此题吗?示例:
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:
2
3
4
5
6
7
8
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
提示:
1 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4
1 <= k <= nums.length
这个从题目上就说的很直白,滑动窗口的最大值。输入一个数组和一个窗口的长度,然后输出这个窗口依次从左滑动到右时,窗口内的最大值。
这个题目从理解上,比上面这些题目要简单(除了第一个)。因为窗口的长度是固定的,我们在移动时同步移动左右指针即可。唯一的难点在于,怎么选择窗口内的最大值。
循环窗口内所有元素,选择最大值么?当然不是,如果是循环选择最大值的话,那复杂度不就是 O(n*k)了么。
除了同步滑动窗口的左右边界,剩下的就是如何在常数时间内获得窗口内的最大值,这个有点像 leetcode 155 最小栈那个类似,那个是实现一个最小栈,即支持栈的操作,然后可以在常数时间内获取栈内的最小值。这个的话,应该是实现一个最大队列,即支持队列的入队出队,然后在常数时间内获得队列里的最大值。因为这个窗口的滑动本身就是一个队列的操作,滑动一次,就是一个入队出队操作。
这里我们使用双端队列来实现。由于 golang 中没有原生实现双端队列这个结构,因此这里自己简单用链表实现一个。
1 | // -----双端队列实现 begin------- |