并查集的定义
并查集(Union Find):一种树型的数据结构,用于处理一些不交集(Disjoint Sets)的合并及查询问题。不交集指的是一系列没有重复元素的集合。
并查集主要支持两种操作:
- 合并(Union):将两个集合合并成一个集合。
- 查找(Find):确定某个元素属于哪个集合。通常是返回集合内的一个「代表元素」。
- 并查集中的「集」指的就是我们初中所学的集合概念,在这里指的是不相交的集合,即一系列没有重复元素的集合。
- 并查集中的「并」指的就是集合的并集操作,将两个集合合并之后就变成一个集合。合并操作如下所示:
1
{1, 3, 5, 7} ∪ {2, 4, 6, 8} = {1, 2, 3, 4, 5, 6, 7, 8}
- 并查集中的「查」是对于集合中存放的元素来说的,通常我们需要查询两个元素是否属于同一个集合。
根据上文描述,我们就可以定义一下「并查集」结构所支持的操作接口:
- **合并
union(x, y)**:将集合x和集合y合并成一个集合。 - **查找
find(x)**:查找元素x属于哪个集合。他可以用来确定两个元素是否属于同一子集。 - **查找
is_connected(x, y)**:查询元素x和y是否在同一个集合中。
并查集的实现
快速查询:基于数组
在使用「快速查询」思路实现并查集时,我们可以使用数组来表示集合中的元素。
数组元素和集合元素是一一对应的,我们将数组的索引值作为每个元素的集合编号,称为id。然后可以对数组进行以下操作:
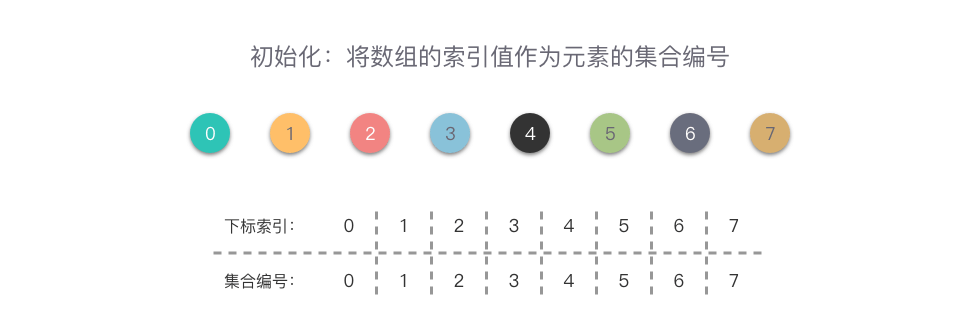
- 初始化:将每个元素的集合编号初始化为数组下标索引,则所有元素的id都是唯一的,代表着每个元素单独属于一个集合。
- 合并操作:需要将其中一个集合中的所有元素id更改为另一个集合中的id,这样能够保证在合并后一个集合中所有元素的id均相同
- 查找操作:如果两个元素的id一样,则说明他们属于同一个集合;反之说明他们不属于同一个集合。
下面我们以集合 {0}, {1}, {2}, {3}, {4}, {5}, {6}, {7} 为例说明:
当我们需要一些合并操作,比如合并为 {0}, {1, 2, 3}, {4}, {5, 6}, {7} ,合并操作如图所示,从图中可以看出,在进行一些列合并操作后,下标为1,2,3的元素集合编号是一致的,这说明3个元素同属于一个集合。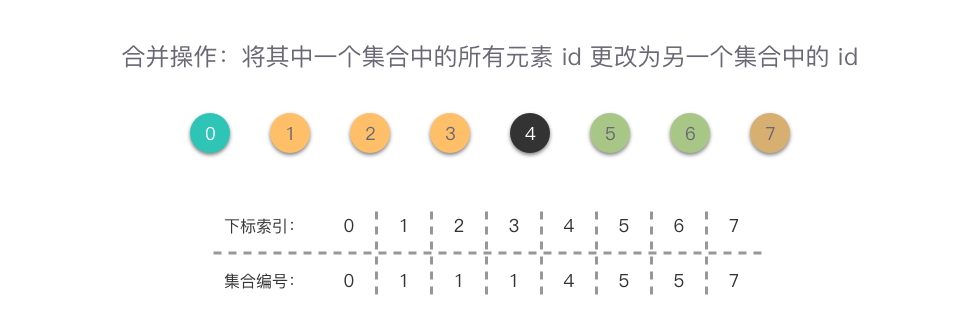
在快速查询的实现思路中,单次查询操作的时间复杂度是 O(1),而单次合并操作的时间复杂度为 O(n)(每次合并操作需要遍历数组)。两者的时间复杂度相差得比较大,完全牺牲了合并操作的性能。因此,这种并查集的实现思路并不常用。
实现代码大致如下:
1 | class UnionFindSet { |
比如要生成上面图示的集合:
1 | const ufset = new UnionFindSet(8); |
合并操作:
1 | // 合并1,2 |
快速合并:基于森林实现
在使用「快速合并」思路实现并查集时,我们可以使用「一个森林(若干棵树)」来存储所有集合。每一棵树代表一个集合,树上的每个节点都是一个元素,树根节点为这个集合的代表元素。
注意:与普通的树形结构(父节点指向子节点)不同的是,基于森林实现的并查集中,树中的子节点是指向父节点的。
此时,我们仍然可以使用一个数组 fa 来记录这个森林。我们用 fa[x] 来保存 x 的父节点的集合编号,代表着元素节点 x 指向父节点 fa[x]。
当初始化时,fa[x] 值赋值为下标索引 x。在进行合并操作时,只需要将两个元素的树根节点相连接(fa[root1] = root2)即可。而在进行查询操作时,只需要查看两个元素的树根节点是否一致,就能知道两个元素是否属于同一个集合。
总结一下,我们可以对数组 fa 进行以下操作来实现并查集:
- 当初始化时:将每个元素的集合编号初始化为数组
fa的下标索引。所有元素的根节点的集合编号不一样,代表着每个元素单独属于一个集合。 - 合并操作时:需要将两个集合的树根节点相连接。即令其中一个集合的树根节点指向另一个集合的树根节点(
fa[root1] = root2),这样合并后当前集合中的所有元素的树根节点均为同一个。 - 查找操作时:分别从两个元素开始,通过数组
fa存储的值,不断递归访问元素的父节点,直到到达树根节点。如果两个元素的树根节点一样,则说明它们属于同一个集合;如果两个元素的树根节点不一样,则说明它们不属于同一个集合。
还是以元素集合 {0}, {1}, {2}, {3}, {4}, {5}, {6}, {7} 作为示例: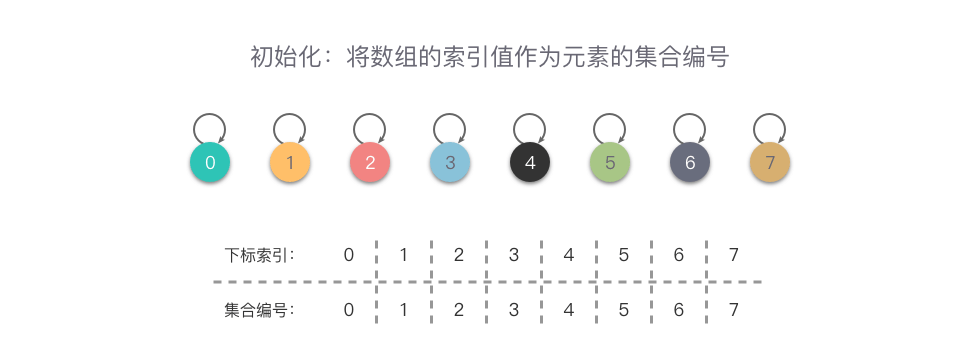
当我们进行一系列的合并操作后,比如 union(4, 5)、union(6, 7)、union(4, 7) 操作后变为 {0}, {1}, {2}, {3}, {4, 5, 6, 7},合并操作的步骤及结果如下图所示。从图中可以看出,在进行一系列合并操作后,fa[4] == fa[5] == fa[6] == fa[fa[7]],即 4、5、6、7 的元素根节点编号都是 4,说明这 4 个 元素同属于一个集合。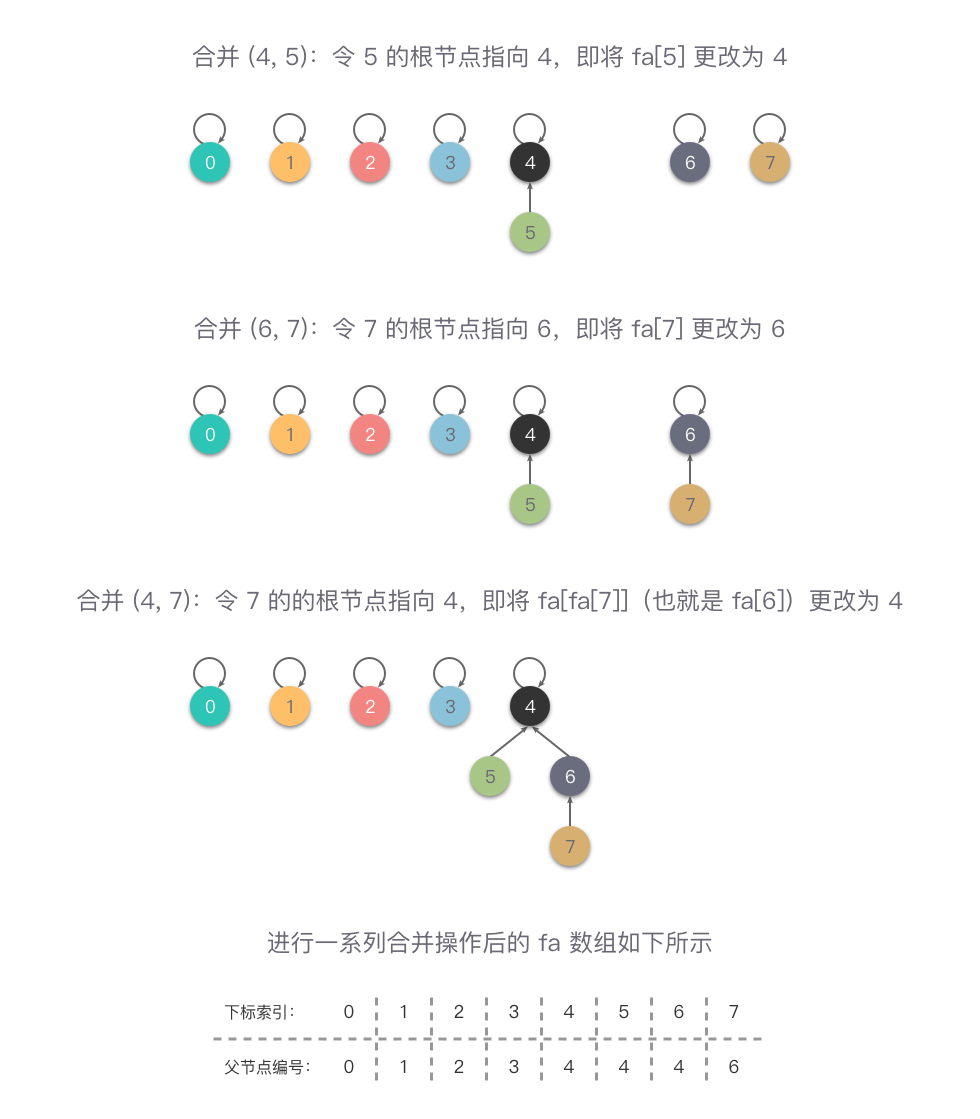
代码实现:
1 | class UnionFindSet { |
路径压缩
在集合很大或者树很不平衡时,使用上述「快速合并」思路实现并查集的代码效率很差,最坏情况下,树会退化成一条链,单次查询的时间复杂度高达 O(n)。并查集的最坏情况如下图所示。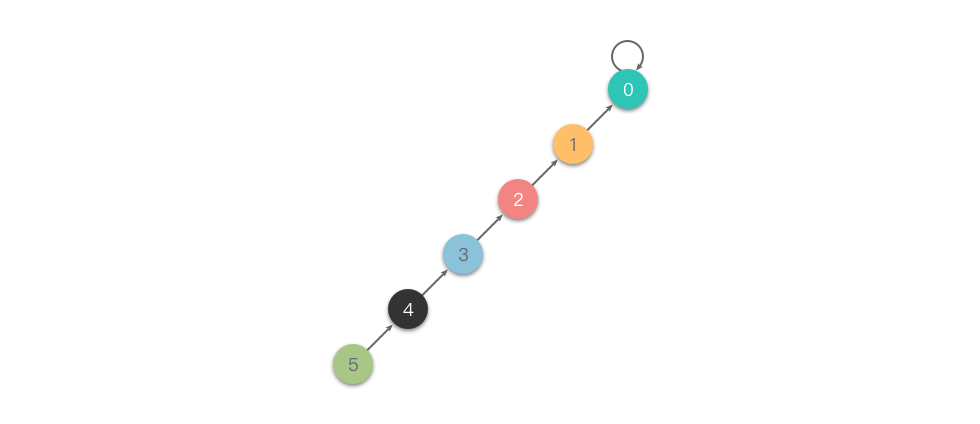
为了避免出现最坏情况,一个常见的优化方式是「路径压缩」。
路径压缩(Path Compression):在从底向上查找根节点过程中,如果此时访问的节点不是根节点,则我们可以把这个节点尽量向上移动一下,从而减少树的层树。这个过程就叫做路径压缩。
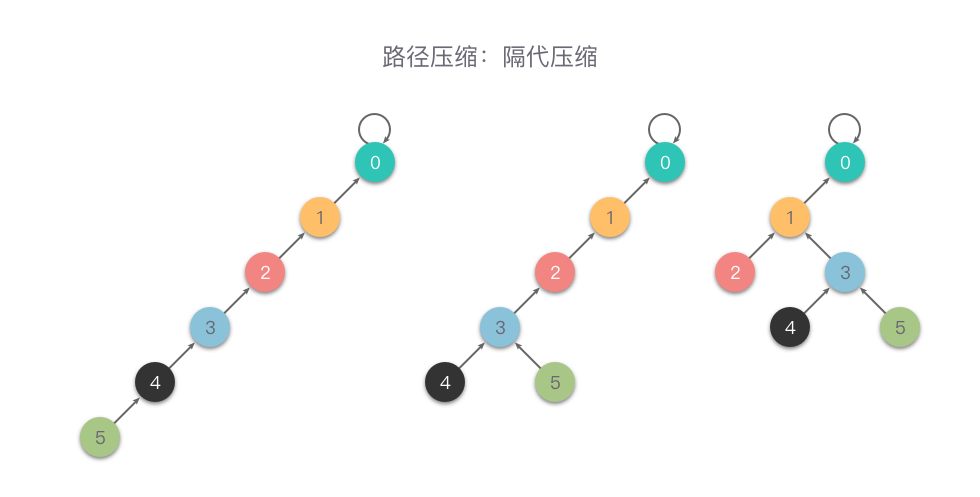
路径压缩有两种方式:一种叫做「隔代压缩」;另一种叫做「完全压缩」。
隔代压缩
隔代压缩:在查询时,两步一压缩,一直循环执行「把当前节点指向它的父亲节点的父亲节点」这样的操作,从而减小树的深度。
隔代压缩的查找代码:
1 | // 查找元素根节点 |
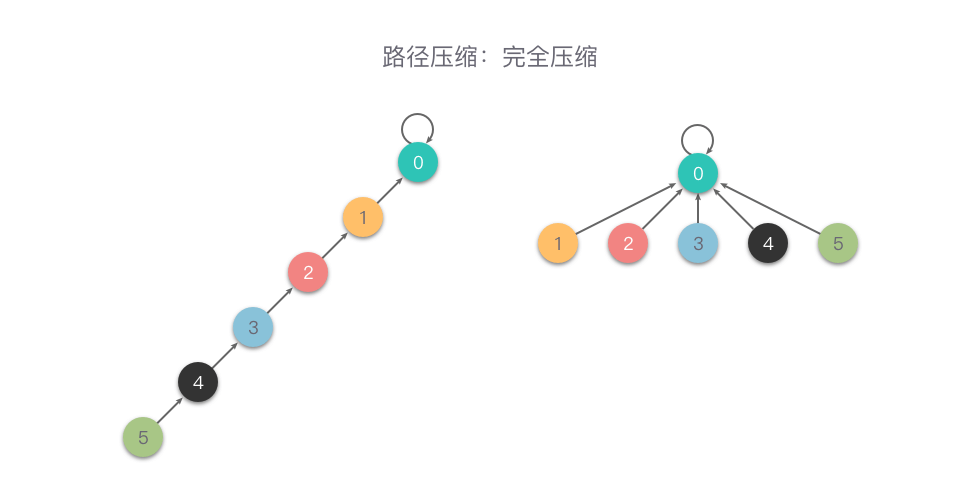
完全压缩
完全压缩:在查询时,把被查询的节点到根节点的路径上的所有节点的父节点设置为根节点,从而减小树的深度。也就是说,在向上查询的同时,把在路径上的每个节点都直接连接到根上,以后查询时就能直接查询到根节点。
相比较于「隔代压缩」,「完全压缩」压缩的更加彻底。下面是一个「完全压缩」的例子。
完全压缩的查找代码实现:
1 | // 查找元素根节点 |
按秩合并
因为路径压缩只在查询时进行,并且只压缩一棵树上的路径,所以并查集最终的结构仍然可能是比较复杂的。为了避免这种情况,另一个优化方式是「按秩合并」。
按秩合并(Union By Rank):指的是在每次合并操作时,都把「秩」较小的树根节点指向「秩」较大的树根节点。
这里的「秩」有两种定义,一种定义指的是树的深度;另一种定义指的是树的大小(即集合节点个数)。无论采用哪种定义,集合的秩都记录在树的根节点上。
按秩合并也有两种方式:一种叫做「按深度合并」;另一种叫做「按大小合并」。
按深度合并
按深度合并(Unoin By Rank):在每次合并操作时,都把「深度」较小的树根节点指向「深度」较大的树根节点。
我们用一个数组 rank 记录每个根节点对应的树的深度(如果不是根节点,其 rank 值相当于以它作为根节点的子树的深度)。
初始化时,将所有元素的 rank 值设为 1。在合并操作时,比较两个根节点,把 rank 值较小的根节点指向 rank 值较大的根节点上合并。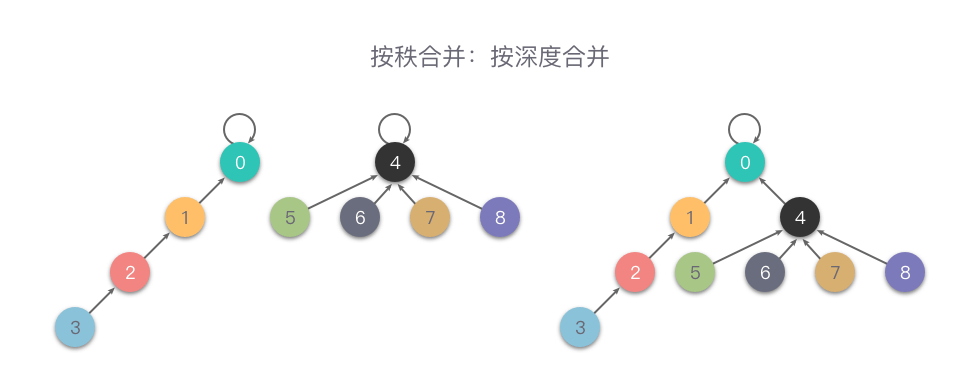
按深度合并的完整代码:
1 | class UnionFindSet { |
按大小合并
按大小合并(Unoin By Size):这里的大小指的是集合节点个数。在每次合并操作时,都把「集合节点个数」较少的树根节点指向「集合节点个数」较大的树根节点。
我们用一个数组 size 记录每个根节点对应的集合节点个数(如果不是根节点,其 size 值相当于以它作为根节点的子树的集合节点个数)。
初始化时,将所有元素的 size 值设为 1。在合并操作时,比较两个根节点,把 size 值较小的根节点指向 size 值较大的根节点上合并。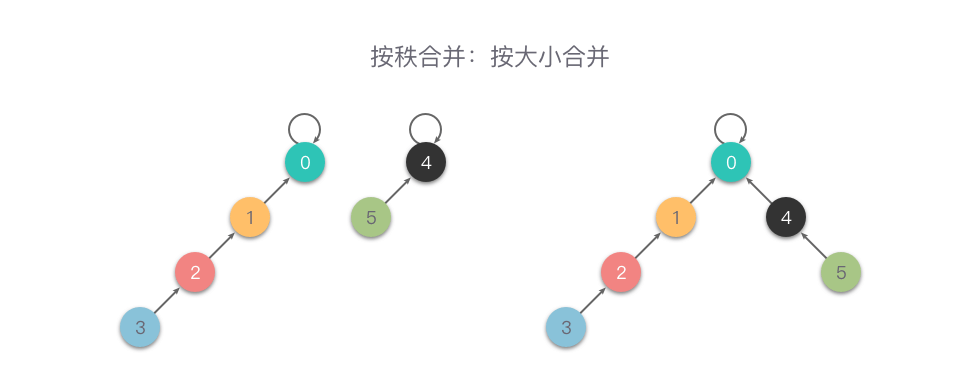
按大小合并完整代码:
1 | class UnionFindSet { |
按秩合并的注意
看过「按深度合并」和「按大小合并」的实现代码后,大家可能会产生一个疑问:为什么在路径压缩的过程中不用更新 rank 值或者 size 值呢?
其实,代码中的 rank 值或者 size 值并不完全是树中真实的深度或者集合元素个数。
这是因为当我们在代码中引入路径压缩之后,维护真实的深度或者集合元素个数就会变得比较难。此时我们使用的 rank 值或者 size 值更像是用于当前节点排名的一个标志数字,只在合并操作的过程中,用于比较两棵树的权值大小。
换句话说,我们完全可以不知道每个节点的具体深度或者集合元素个数,只要能够保证每两个节点之间的深度或者集合元素个数关系可以通过 rank 值或者 size 值正确的表达即可。
而根据路径压缩的过程,rank 值或者 size 值只会不断的升高,而不可能降低到比原先深度更小的节点或者集合元素个数更少的节点还要小。所以,rank 值或者 size 值足够用于比较两个节点的权值,进而选择合适的方式进行合并操作。
并查集的算法分析
首先我们来分析一下并查集的空间复杂度。在代码中,我们主要使用了数组 fa 来存储集合中的元素。如果使用了「按秩合并」的优化方式,还会使用数组 rank 或者数组 size 来存放权值。因为空间复杂度取决于元素个数,不难得出空间复杂度为 O(n)。
在同时使用了「路径压缩」和「按秩合并」的情况下,并查集的合并操作和查找操作的时间复杂度可以接近于 O(1)。最坏情况下的时间复杂度是 O(m∗a(n))。这里的 m 是合并操作和查找操作的次数,a(n) 是 Ackerman 函数的某个反函数,其增长极其缓慢,也就是说其单次操作的平均运行时间可以认为是一个很小的常数。
总结一下:
- 并查集的空间复杂度:O(n)。
- 并查集的时间复杂度:O(m∗a(n))。
并查集的应用
并查集通常用来求解不同元素之间的关系问题,比如判断两个人是否是亲戚关系、两个点之间时候存在至少一条路径连接。或者用来求解集合的个数、集合中元素的个数等等。