字符串匹配算法-Rabin Karp算法

发表于   |   分类于 ，

一个很简单的问题，给定一个字符串txt和一个模式串pat，写一个函数search来输出字符串txt中所有和pat相等的子串。

例如，给定txt=”this is a test text”， pat=”text”，返回 [10]

这个问题非常简单，我们只需要暴力穷举所有txt中所有长度等于len(pat)的子串，并判断其是否和pat相等即可。相等就返回其起始索引。

在判断子串是否和pat相等时，我们需要逐位去比较。这样，这个问题的复杂度就是 O(mn)。这种算法我们称为朴素字符串匹配算法。

很显然，这样的算法效率并不高。

Rabin Karp算法即是解决这个问题的更高效的一个算法。它的思想是，不直接逐位对比模式串pat和text是否相等，而是利用哈希算法，计算模式串和子串的哈希值，如果哈希值不相等，那么很明显字符串也不相等，如果相等，由于哈希算法可能会存在哈希冲突的可能，因此我们需要再使用朴素算法判断其是否真正相等。

可能有的人会问，计算字符串的哈希值，不也要逐位计算，然后才能算出一个哈希值，那这样复杂度不还是O(mn)么？

对了，Rabin Karp算法的核心是，将哈希函数使用滚动哈希来计算，这样计算哈希的复杂度是O(1)，整体的复杂度就变成了O(m)了。

这里我们先把Rabin Karp使用的哈希算法放一边，思考一下如果是我们自己，应该怎样选择一个哈希算法呢？

对于一个只含有数字的字符串“123”来说，普通人第一眼的感觉不应该是，这是一个数字，123。

而且字符串”123”和字符串”234”是不相等的，因为其代表的数字123和234是不相等的。

这里就有点上面所说的哈希的意味了，我们不直接对比字符串的每个字符，而是比较其所代表的数字是否相等即可。

我们知道，对于一个只有数字的字符串a[0]a[1]a[2]...a[n]要转换成十进制的数字，公式如下：

num = a[n]*10^0 + a[n-1]*10^1 + a[n-2]*10^2 + ... + a[1]*10^(n-1) + a[0]*10^n

在此基础上，我们往外延伸，如果对于一个只有小写英文字符的字符串来说，我们是不是可以当成26进制，然后计算出一个字符串所代表的数字：

num = a[n]*26^0 + a[n-1]*26^1 + a[n-2]*26^2 + ... + a[1]*26^(n-1) + a[0]*26^n

其中上面的这个公式，我们就可以作为计算哈希的公式。使用这个计算哈希会把复杂度降到O(1)么?

会，我们来看一下为什么。

比如对于一个字符串”abcd”，我们要计算一个长度为2的子串的子串的哈希，先计算”ab”的：
hash1 = code(a)*26^1 + code(b)*26^0

再计算”bc”的：
hash2 = code(b)*26^1 + code(c)*26^0

看一下这里的规律，在计算hash2时，我们完全可以复用hash1的值，hash2=(hash1-code(a)*26^1)*26+code(c)*26^0

已知前一个子串的哈希值，计算后一个哈希值的过程，如下：

当然，如果字符串过长，最后计算哈希可能会溢出。为了解决这个问题，在Rabin-Karp算法中，求哈希时，使用取余。

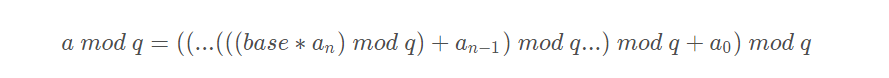
20200430170918965

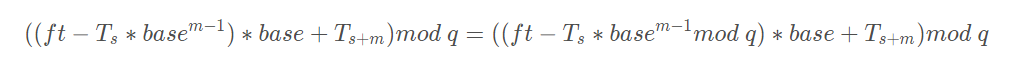
20200430170945852

即：

hash( txt[s+1 .. s+m] ) = ( d ( hash( txt[s .. s+m-1]) – txt[s]*h ) + txt[s + m] ) mod q
hash( txt[s .. s+m-1] ) : Hash value at shift s.
hash( txt[s+1 .. s+m] ) : Hash value at next shift (or shift s+1)
d: Number of characters in the alphabet
q: A prime number
h: d^(m-1)

Java代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
// Following program is a Java implementation 
// of Rabin Karp Algorithm given in the CLRS book 

public class Main 
{ 
	// d is the number of characters in the input alphabet 
	public final static int d = 256; 
	
	/* pat -> pattern 
		txt -> text 
		q -> A prime number 
	*/
	static void search(String pat, String txt, int q) 
	{ 
		int M = pat.length(); 
		int N = txt.length(); 
		int i, j; 
		int p = 0; // hash value for pattern 
		int t = 0; // hash value for txt 
		int h = 1; 
	
		// The value of h would be "pow(d, M-1)%q" 
		for (i = 0; i < M-1; i++) 
			h = (h*d)%q; 
	
		// Calculate the hash value of pattern and first 
		// window of text 
		for (i = 0; i < M; i++) 
		{ 
			p = (d*p + pat.charAt(i))%q; 
			t = (d*t + txt.charAt(i))%q; 
		} 
	
		// Slide the pattern over text one by one 
		for (i = 0; i <= N - M; i++) 
		{ 
	
			// Check the hash values of current window of text 
			// and pattern. If the hash values match then only 
			// check for characters on by one 
			if ( p == t ) 
			{ 
				/* Check for characters one by one */
				for (j = 0; j < M; j++) 
				{ 
					if (txt.charAt(i+j) != pat.charAt(j)) 
						break; 
				} 
	
				// if p == t and pat[0...M-1] = txt[i, i+1, ...i+M-1] 
				if (j == M) 
					System.out.println("Pattern found at index " + i); 
			} 
	
			// Calculate hash value for next window of text: Remove 
			// leading digit, add trailing digit 
			if ( i < N-M ) 
			{ 
				t = (d*(t - txt.charAt(i)*h) + txt.charAt(i+M))%q; 
	
				// We might get negative value of t, converting it 
				// to positive 
				if (t < 0) 
				t = (t + q); 
			} 
		} 
	} 
	
	/* Driver program to test above function */
	public static void main(String[] args) 
	{ 
		String txt = "GEEKS FOR GEEKS"; 
		String pat = "GEEK"; 
		int q = 101; // A prime number 
		search(pat, txt, q); 
	} 
} 

// This code is contributed by nuclode