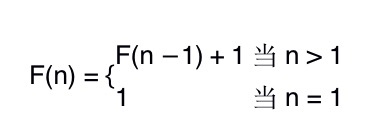聊聊算法之递归

递归在编程时，是一项非常有用的思想，对分析问题很有帮助。可是在面试聊候选人的时候发现，很多人对递归的认识不是很到位，经常得到的回答就是“递归就是自己调用自己啊”这样的回答。然而在什么情况下用递归，或者递归解决了什么样的问题等，基本就回答不上来了。

递归虽然很简单，但也不至于简单到，“递归就是自己调用自己啊”这种程度。

这篇文章也是自己的一份整理总结吧，对自己知识的巩固。

什么是递归

递归是一种解决问题的思路和方法，把问题分解成规模更小的子问题，而这些子问题又与原问题有着相同解法。这是一种思维模型，而大家经常所说的“自己调用自己”仅仅是在代码实现时的表象而已。

递归有两个重要的条件：

1. 拆分原问题为规模更小的子问题，并且这些子问题解决模型和原问题相同
2. 存在终止条件。这个点非常重要，对于拆分的这些子问题，必然存在一种简单的情况能够得出该子问题的结果。

递归，从名称上，可以看出，存在两个动作，递和归。其中“递”是在解决原问题时，要先解决其拆分的子问题，这时由解决原问题“递向”解决子问题。“归”是指解决完子问题后，要回来继续解决原问题。也就是说，上面说的递归的两个条件中的第二个，存在终止条件即是存在于“递”和“归”这两个过程的中间，先“递”，到达终止条件，再“归”。

大家经常举的递归的例子，最多的都是斐波那契数列，或者是 n!计算 n 的阶乘这样的数学上的问题，因为这种问题有计算公式，写出来非常直观，确实是自己调自己，这也是为什么很多人对于对归的理解仅仅局限于“自己调自己”了。

那我们来举一个生活中的场景来理解什么是递归。

假如你去看电影，坐在最后一排。这个时候，你想知道你坐的第几排，有一种办法是，自己站起来从前面开始数对吧，但是这种方法要你站起来走到第一排，很累啊，懒惰的你，想到一种简单的方法，问问前面一排的人是第几排，你不就知道了自己在第几排了么！于是，你问你前面一排的人，“你是第几排呀？”，前面这哥们，也不知道自己是第几排，于是乎，采用了同样的方式，问他前面一排的人，“你是第几排呀？”，就这样，一直往前问，一直问到第一排，好嘛，第一排的哥们一看自己前面没人了呀，肯定知道自己是第一排，于是说，第 1️⃣ 排，而后，他后面的就知道了，那我是第二排呀，于是乎，又这样返回回来，你前面的哥们回来跟你说，我是第 9️⃣ 排，那你就知道了，自己是第 🔟️ 排。

这就是递归。

递的过程，是你要想知道自己是第几排，于是你就问前面的哥们是第几排，前面的哥们再往前问，这个过程就是“递”。当问到第一排时，第一排的哥们知道自己前面没人了，也就之道自己是第一排，于是说自己是第一排，这里就是遇到了递归过程的终止条件。第二排的哥们得知自己前面的是第一排，那么自己肯定是第二排，第三排的知道自己前面是第二排，那自己肯定是第三排，依次往后传，这个过程就是“归”的过程。当传到你的时候，你就知道自己在第几排，也就是解决了问题，这整个过程就是使用递归的思想来解决问题的过程。

来看看这个过程，怎么和递归的思想对应起来：

1. 拆分问题。你想知道自己在第几排，你想到的是，如果我知道了前面哥们在第几排，我不就知道我在第几排了么？这就是将大问题拆分为更小问题的过程，而这些小问题和原问题又有着相同的解决思路，前面的哥们不知道，可以问他前面的。这就是“递”的过程，把问题往前递。
2. 终止条件。当问到第一排的哥们时，由于第一排的哥们前面没有人了，此时他肯定知道自己在第一排。这也就是遇到了问题的终止条件。

这个问题，如果用数学公式去表达，可以描述为：

假设 f(n) 表示要问的人在第几排

如何解决递归问题

1. 拆分问题，写出递归公式
2. 找到递归的终止条件

一般在解决实际问题时，如果一个问题能用递归解决，思路是先拆分子问题，找出子问题的解决公式，然后再找到终止条件，最后根据这些写出数学公式，有了这些公式，其实写代码时，也就直接去翻译这个公式即可。

递归的 🌰️

1. 爬楼梯

小明上台阶，一次只能上 1 个或 2 个台阶，问，对于有 n 个台阶的楼梯，小明总共有多少种走法。

这个问题，在我前一篇关于动态规划的博文中有提及，当时使用来说明动态规划类问题，有兴趣的可以看看。

1. 拆分子问题，写递归公式。
   对于第 n 个台阶，由于小明一次只能上 1 个或 2 个台阶，那么他肯定有两种方法上来，从 n-1 个台阶走 1 步上来，或者从 n-2 个台阶走两步上来。
   也就是说，f(n)=f(n-1)+f(n-2)
2. 找到终止条件
   这个问题的终止条件在哪呢？有时候如果终止条件不是那么明确，其实可以从公式推导出来，比如这个问题。由于 f(n)=f(n-1)+f(n-2)，那么 n 的最小值肯定为 2，因为 n 再小就会发生溢出了，所以这里终止条件有两个，n=1 和 n=2。如果只有一个台阶，那么很明显就一种方法，走一步上来即可。如果两个台阶，那么他可以直接走 2 步上来，也可以一次走一步，走两次上来，总共 2 中方法，也就是有了终止条件 f(1)=1,f(2)=2.

有了公式和终止条件，写代码就好说了。

func climbStairs(n int) int {
    if n == 1 || n == 2 {
        return n
    }

    return climbStairs(n-1) + climbStairs(n-2)
}

2. 斐波那契数列

来一个经典的讲述递归的栗子，斐波那契数列。斐波那契数列是这样一个数列，它的后一个数是前两个数的和，形如：1,1,2,3,5,8,13,21,34……..
要求写一个程序，输出斐波那契数列的第 n 个数。

根据定义，我们得知，在斐波那契数列中的某一项，是前两项的和，可以写出公式 f(n)=f(n-1)+f(n-2)，这个公式和上面这个爬楼梯的栗子的公式是一样的。终止条件，通过数列，我们可以得知 f(1)=1,f(2)=1,因此，最终的代码和上面是一样的，只需要改一下终止条件即可。

func fib(n int) int {
    if n == 1 || n == 2 {
        return 1
    }

    return fib(n-1) + fib(n-2)
}

递归思想在数据结构以及经典算法中的应用

1. 链表

链表这个结构无需多言，本身其结构在定义的时候，就是符合递归的。所以，在链表的很多问题上，我们其实是可以直接使用递归来解决的。

链表的遍历

type LinkedListNode struct {
    data int
    next *LinkedListNode
}

func visit(node *LinkedListNode) {
    if node == nil {
        return
    }
    fmt.Printf("%d\t", node.data)
    visit(node.next)
}

统计链表节点个数

递归的统计链表的节点个数，其实很简单。和遍历一样，遇到节点，我们就加 1 即可。这里的终止条件就是链表的最后一个节点，因为最后一个节点再无后继节点。

其实，对于链表的各种递归操作，其终止条件一般都是链表的最后一个节点，因为最后一个节点再无后继节点。也就是链表的递归定义的终止条件。

func count(node *LinkedListNode) int {
    if node == nil {
        return 0
    }
    return 1 + count(node.next)
}

链表的反转操作

对于一个链表1->2->3->4->5，将其反转得到5->4->3->2->1。

链表的反转操作，其实就是找到当前节点的下一节点，然后将下一节点的 next 指向当前节点，然后当前节点的 next 指向上一节点。

终止条件就是链表的最后一个节点，因为最后一个节点后面再无其他节点，因此后面无需再反转。

type LinkedListNode struct {
    data int
    next *LinkedListNode
}
func reverse(node *LinkedListNode) *LinkedListNode {
    if node == nil || node.next == nil {
        return node
    }

    // 找到终止条件，这里是最后一个节点
    head := reverse(node.next)

    // 节点反转操作
    next := node.next
    next.next = node
    node.next = nil

    return head
}

链表的间隔反转

上面那个反转是将整个链表反转，这个栗子是将链表中相邻的两个元素进行反转。比如1->2->3->4->5反转得到2->1->4->3->5。

这个也很简单，在反转的过程中，隔一个节点，反转一次即可。

func reverseNext(node *LinkedListNode) *LinkedListNode {
    if node == nil || node.next == nil {
        return node
    }

    next := node.next
    node.next = reverseNext(next.next)
    next.next = node

    return next
}

2. 二叉树

二叉树的定义就是递归的。二叉树有左右两个子树，左右两个子树也是二叉树。因此二叉树的很多操作，使用递归方式更直观，也更简单。比如下面几个操作。

二叉树的遍历

二叉树的遍历根据访问根节点的顺序有 3 种，先序遍历，中序遍历，后序遍历。对下面一棵树而言：

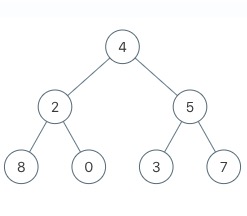
// 二叉树节点的定义
type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

• 先序遍历：先访问根节点，然后再依次访问左右子树。

func preOrder(node *TreeNode) {
    if node == nil {
        return
    }
    fmt.Printf("%d\t", node.Val)
    preOrder(node.Left)
    preOrder(node.Right)
}
// 4       2       8       0       5       3       7

• 中序遍历：先访问左子树，再访问根节点，最后访问右子树。

func inOrder(node *TreeNode) {
    if node == nil {
        return
    }
    inOrder(node.Left)
    fmt.Printf("%d\t", node.Val)
    inOrder(node.Right)
}
// 8       2       0       4       3       5       7

• 后序遍历：先访问左右子树，最后再访问根节点。

func postOrder(node *TreeNode) {
    if node == nil {
        return
    }
    postOrder(node.Left)
    postOrder(node.Right)
    fmt.Printf("%d\t", node.Val)
}
// 8       0       2       3       7       5       4

检查二叉树是否镜像对称（LeetCode-101）

给定一棵二叉树，检查是否是镜像对称的。什么是对称的，就是左右子树对称，例如下面这个就是对称的：

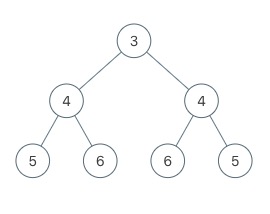
这个问题，其实从问题本身的描述上，就能看出可以用递归来解决。

func compareNode(node1 *TreeNode, node2 *TreeNode) {
    if node1 == nil && node2 == nil {
        return true
    }
    if node1 == nil || node2 == nil {
        return false
    }
    return node1.Val == node2.Val && compareNode(node1.Left, node2.Right) && compareNode(node1.Right, node2.Left)
}

func isSymmetric(root *TreeNode) bool {
    if root == nil {
        return true
    }
    return compareNode(root.Left, root.Right)
}

因为要对比左右子树，所以，这里要写一个对比函数 compareNode(left, right)接收两个要对比的节点。在这个方法里，我们要检查两个节点的值是否相等，如果相等，再递归的检查两个节点的子树是否相等。检查两个节点的子树是否相等时，由于要求对称，因此对比的是两个节点的左右子树交叉对比，即 node1.Left 要和 node2.Right 对比，node1.Right 要和 node2.Left 左对比。

二叉树的最大深度（LeetCode-104）

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

func visit(root *TreeNode, depth int) int {
    if root == nil {
        return depth
    }

    left := visit(root.Left, depth+1)
    right := visit(root.Right, depth+1)
    if left > right {
        return left
    }
    return right

}

func maxDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    return visit(root, 0)
}

要计算二叉树的深度，相当于要计算叶子节点的高度。因此，在遍历访问时，我们要加上一个标识节点高度的参数 level。根节点的高度就是 0，访问其子节点时，level 加 1，然后递归的访问其左右子树的高度，返回左右子树的最大高度即可。

终止条件就是遇到叶子节点。因为叶子节点没有子节点了，无法再继续访问了。

将有序数组转换成高度平衡的二叉搜索树(LeetCode-108)

给定一个有序数组，将其转换成一个高度平衡的二叉搜索树。
一个高度平衡二叉树是指一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1。

由于给定的数组已经是按照升序排好序的数组，那么按照二叉搜索树的定义，只需要把数组中间位置的元素作为根节点，左边元素作为树的左子树，右边元素作为树的右子树即可。

说到这里，用递归就不言而喻了。将数组中间位置元素作为根节点，左边元素再递归的构建左子树，右边元素递归的构建右子树即可。

func createNode(num int) *TreeNode {
    node := new(TreeNode)
    node.Val = num
    return node
}
func sortedArrayToBST(nums []int) *TreeNode {
    length := len(nums)
    if length == 0 {
        return nil
    }
    head := createNode(nums[len(nums)/2])
    head.Left = sortedArrayToBST(nums[:len(nums)/2])
    head.Right = sortedArrayToBST(nums[len(nums)/2+1:])
    return head
}

二叉树的最小深度（LeetCode-111）

这个问题和上面最大深度正好相反，上面是要求二叉树的最大深度，而这个是要求最小深度。

树的最小深度是从根节点开始到所有叶子节点的所有路径中最小路径。

所以，这里的解决办法，和上面的很类似，可以直接套用上面那个思路即可。

func visit(root *TreeNode, level int, min *int) {
    if root.Left == nil && root.Right == nil {
        if *min > level {
            *min = level
        }
        return
    }
    if root.Left == nil {
        visit(root.Right, level+1, min)
        return
    }
    if root.Right == nil {
        visit(root.Left, level+1, min)
        return
    }

    visit(root.Left, level+1, min)
    visit(root.Right, level+1, min)

}

// 遍历二叉树，遇到叶子节点，判断当前节点的路径是否最小
func minDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    min := math.MaxInt32
    visit(root, 1, &min)
    return min
}

这里额外写了一个访问方法 visit()，三个参数，第一个是要访问的树节点，第二个是该节点所属的层数，第三个是一个 int 类型的指针，用以记录最小路径。

如果遇到叶子节点（左右子树均为空），判断当前节点的层级（代表此节点的路径）和当前记录的最小路径比较，如果比当前最小路径还小，则该路径记为最小路径。如果不是叶子节点，继续访问其子树。

在 minDepth()函数中定义一个最小值，使用 math 库里的 MaxInt32 作为最小值。然后开始访问树的根节点，访问完即可。

判断二叉树是否高度平衡二叉树（LeetCode-110）

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1。

// 判断某个节点是否平衡，并记录其节点深度
func balanced(root *TreeNode, depth *int) bool {
    if root == nil {
        *depth = 0
        return true
    }
    left, right := 0, 0
    leftBalanced, rightBalanced := balanced(root.Left, &left), balanced(root.Right, &right)
    if leftBalanced && rightBalanced {
        gap := left - right
        if gap <= 1 && gap >= -1 {
            if left > right {
                *depth = left + 1
            } else {
                *depth = right + 1
            }
            return true
        }
    }
    return false
}
func isBalanced(root *TreeNode) bool {
    if root == nil {
        return true
    }
    depth := 0
    return balanced(root, &depth)
}

要想判断一棵二叉树是否高度平衡的，我们要找到所有的叶子节点的高度，检查其最大高度以及最小高度的差是否小于等于 1 即可。

这里我们写一个 balanced()函数做辅助，函数在判断一个节点是否平衡的同时，记录其所在根节点的深度。
如果节点平衡，记录其深度，如果不平衡，那么直接返回 false 即可，就没必要再记录其深度了。
然后递归判断这个子节点的左右子节点是否平衡。

3. 二分查找

二分查找是在一个有序的数组上进行查找，采用分治的方法将遍历查找的时间复杂度从 O(n)优化到 O(lgn)。
二分查找采用分治的方法，也就是不断缩小查找的规模，在此过程中，也是符合递归的思想，采用递归的模型来解决。

func search(nums []int, start, end int, target int) int {
    if start > end {
        return -1
    }
    mid := (start + end) / 2
    if nums[mid] == target {
        return mid
    }
    if nums[mid] > target {
        return search(nums, start, mid-1, target)
    }
    if nums[mid] < target {
        return search(nums, mid+1, end, target)
    }
    return -1
}
func binarySearch(nums []int, target int) int {
    if len(nums) == 0 {
        return -1
    }
    return search(nums, 0, len(nums)-1, target)
}

按照二分查找分治的思想，我们先写一个 search 函数，接收四个参数，nums 要查找的数组，start,end 表示要查找的子数组的起始结束位置，target 表示要查找的目标值。我们要判断在 start,end 中间位置 mid 处的元素和目标值 target 的大小，如果目标值小，则要查找 start, mid-1 子数组，如果目标值大，则再继续查找 mid+1,end 子数组。递归的终止条件就是 mid 处的元素和目标值相同或 start 和 end 交汇即是终止，因为此时已无子数组可供查询。

4. 归并排序

归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

归并排序时，将数组分为左右两个子数组，然后再递归的将左右两个子数组调用递归排序，最后将左右两个已排好序的数组再合并成一个数组。基于此思想，这里也用到了递归。

func mergeSort(r []int) []int {
    length := len(r)
    if length <= 1 {
        return r
    }
    num := length / 2
    left := mergeSort(r[:num])
    right := mergeSort(r[num:])
    return merge(left, right)
}
func merge(left, right []int) (result []int) {
    l, r := 0, 0
    for l < len(left) && r < len(right) {
        if left[l] < right[r] {
            result = append(result, left[l])
            l++
        } else {
            result = append(result, right[r])
            r++
        }
    }
    result = append(result, left[l:]...)
    result = append(result, right[r:]...)
    return
}

递归的效率问题以及优化

列举了那么多的例子，无非就是想说明递归思想在编程领域的重要性。但递归也不是完美的，它也存在它的弊端。效率遍是其中一个。
我们拿上面那个斐波那契数列的例子来说，我们得到的递归公式是 fib(n)=fib(n-1) + fib(n-2)，这个公式会造成很多的重复计算，什么意思呢？我们来看看如果计算 fib(5)，这个公式是怎么运行的：

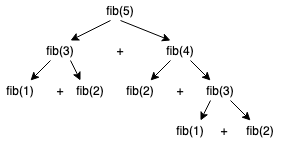
看到没，在计算 fib(5)的过程中，fib(1)被重复计算 2 次，fib(2)被重复计算 3 次，fib(3)被重复计算 2 次，本来只需计算 5 次，却被重复计算那么多次。随着计算深度的增加，重复计算的值只会更多。这样会导致计算效率会很低下。
而且，由于程序语言在函数调用时，会使用栈来保存临时变量。栈这个数据结构，先进后出。如果递归的层次很深，程序一直入栈而不出栈，那么就可能会发生栈内存溢出，也就是大家经常说的“爆栈”。

递归是一种常见的思维模型，用递归的方式去解决一些问题会简洁明了很多，但是上面也说到了其两个缺点，那怎么优化呢？

有一种方案就是，采用尾递归。尾递归就是将之前子问题的结果一并带入下一次递归运算，这样就避免了重复计算的问题。
还是用斐波那契数列的例子来说，该如何改写为尾递归的形式呢？fib(n)=fib(n-1) + fib(n-2)，那么在计算 fib(n)时，要将 fib(n-1)和 fib(n-2)的值一并带进来，而不重新计算。改写的代码如下：

func fib(pre1, pre2, n int) int {
    if n == 3 {
        return pre1 + pre2
    }
    return fib(pre2, pre1+pre2, n-1)
}

重写的 fib 函数接收三个参数，pre1,pre2 表示公式中的用到的前两个数，n 表示要计算第 n 项。这样相当于减少了重复计算，也减少了调用栈。

尾递归的本质是：将单次计算的结果缓存起来，传递给下次调用，相当于自动累积。

还有一种方式就是迭代替换递归。当然，这里所说的替代其实是用迭代的写法来替换自调用的方式，其实递归只是一种思考问题的模型，这里并不影响我们讨论递归。
比如，斐波那契数列如果用迭代的写法，如下：

func fib(n int) int {
    if n == 1 || n == 2 {
        return 1
    }
    pre1, pre2 := 1, 1
    for i := 3; i <= n; i++ {
        pre1, pre2 = pre2, pre1+pre2
    }
    return pre2
}

使用迭代后，效率是 O(n)，不会存在重复计算，而且即使计算规模再大，也不会出现爆栈(当然，有可能会出现内存溢出，但这不是一个概念)。

至于递归和迭代的不同，有时间再研究研究整理一下。

后记

之前在写关于动态规划的一篇文章中，在分析动态规划时，也提到了动态规划也是将一个大问题，拆分为若干子问题，而且举例时，也用到了上面那个爬楼梯那个，代码也用到了递归，那么，递归和动态规划什么区别，他们有什么不同的应用场景么？有时间在整理一篇文章，重点讨论一下迭代和递归，递归和动态规划在问题建模上的区别及应用。