在leetcode上打家劫舍这个系列也是动态规划的题目,分支变形,难度逐渐加大。今天整理一下这个系列的题目,做个记录。
打家劫舍
小偷在偷窃时,唯一的限制就是,不能同时偷相邻的两个房屋。
我们定义 dp[i] 为偷到第i家时能偷到的最大金额,那么偷到第i家时可能有两种情况:
- 第i-1家偷过,那么当前第i家就不能再偷了,此时
dp[i]=dp[i-1] - 第i-1家没偷过,那么当前第i家是可以偷的,此时
dp[i]=dp[i-2]+nums[i] - 这两种情况,取最大值便是偷到第i家时能够偷到的最大金额
因此,相应的状态转移公式为:
1 | dp[i]= Math.max(dp[i-1], dp[i-2]+nums[i]) |
对于初始状态,dp[0]=nums[0] ,dp[1]=Math.max(nums[0], nums[1])
1 | function rob(nums: number[]): number { |
打家劫舍II
这个题目相比较打家劫舍I而言,多了一个限制,数组为循环数组。也就是说,第一家和最后一家在物理上是挨着的,不能同时偷窃。
因此这个时候有两种情况需要考虑:
- 考虑第一个房子,但不考虑最后一个房子(抢第一个房子,不抢最后一个房子)
- 抢第一个房子,不抢最后一个房子,相当于在
nums[0]...nums[n-2]中进行打家劫舍
- 考虑最后一个房子,但不考虑第一个房子(抢最后一个房子,不抢第一个房子)
- 抢最后一个房子,不抢第一个房子,相当于在
nums[1]...nums[n-1]中进行打家劫舍
- 两种情况取最大值即可
1 | function rob(nums: number[]): number { |
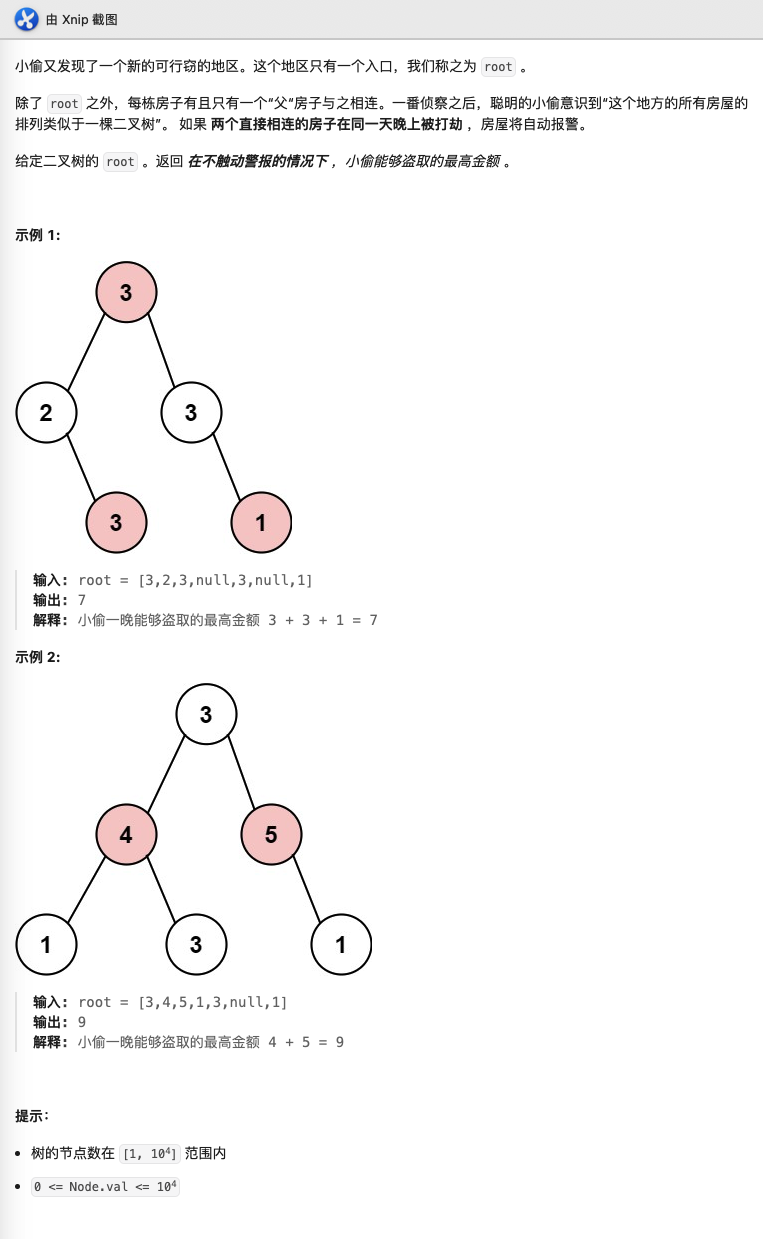
打家劫舍III
这个题目是打家劫舍I和打家劫舍II的升级版,由原来的线性结构升级为二叉树结构。
和上面一样,对于每个节点(房屋),都有两种状态:偷和不偷。
我们用 f(n) 表示偷n节点的情况下,n节点的子树上能够偷到的最大值。
用g(n)表示不偷n节点的情况下,n节点的子树上偷到的最大值。
l和r表示n的左右子树。
- 当n被选偷时,n的左右孩子都不能被偷,故n被选中的情况下子树上被选中点的最大权值和为l和r不被选中的最大值和相加,即
f(n)=g(l)+g(r) - 当n不被偷时,n的左右孩子可以被偷,也可以不被偷。对于n的某个具体的孩子x,它对n的贡献值是x被选中和不被选中情况下权值和的较大值。故
g(n)=max(f(l),g(l))+max(f(r),g(r))注意这里,当n不被偷时,n的左右孩子即可能被偷,也可能不被偷。因为只要求说被偷的房子不连在一起即可,而不是必须间隔。
1 | function rob(root: TreeNode | null): number { |