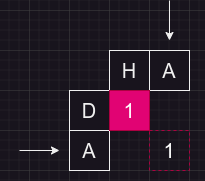
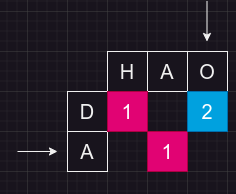
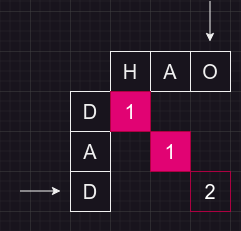
编辑距离是动态规划经典题之一。编辑距离是指给定两个字符串,计算由其中一个字符串通过添加,修改,删除字符操作后转变为另一个字符串所需的最少操作数。
同样,由编辑距离也延伸出来一些变种题目解题思路也是类似,今天就来整理一下这个系列,做个备忘录,方便学习。
编辑距离
对于编辑距离这个题目而言,我们最终并不关心两个字符串经过如何的编辑得到一致,而只关心最终的操作步骤数即可。这也是很多动态规划题目的解决场景,不关心具体步骤,只关心最终状态。
定义状态
同时遍历word1和word2,i指针遍历word1,j指针遍历word2。
我们定义dp[i][j]为字符串 word1 以 i-1 为结尾的的子串word1[:i-1]和字符串 word2 以 j-1 为结尾的子串word[:j-1]的最短编辑距离,那么最终要求的结果便是 dp[word1.length][word2.length]。
那么,对于 word1[i-1] 和 word2[j-1] 比较,有两种情况:
word1[i-1]==word2[j-1],遇到相同的元素,说明不需要编辑,即dp[i][j]=dp[i-1][j-1]word1[i-1]!=word2[j-1],遇到了不同的元素,此时需要编辑操作- 删除 word1 一个元素
word1[i-1],那么就是以 i-2 为结尾的 word1 子串word1[:i-2]与 j-1 为结尾的 word2 的子串word2[:j-1]的最短编辑距离再加上一个操作。即dp[i][j]=dp[i-1][j]+1。 - 删除 word2 一个元素
word2[j-1],那么就是以 j-2 为结尾的 word2 子串word2[:j-2]与 i-1 为结尾的 word1 的子串word1[:i-1]的最短编辑距离再加上一个操作,即dp[i][j]=dp[i][j-1]+1 - 替换 word1 的
word1[i-1]为 word2 的word2[j-1]或者替换word2[j-1]为word1[i-1]。一个替换操作之后,相当于word1[i-1]==word2[j-1],即最终dp[i][j]=dp[i-1][j-1]+1 - 最终取三者最小即可
- 删除 word1 一个元素
上面两个都是删除操作,为什么不是添加操作呢?其实对 word1 进行删除操作就相当于对 word2 进行添加操作,同理,对 word2 进行删除操作就相当于对 word1 进行添加操作。
状态转移方程:
1 | |- dp[i-1][j-1]; 当word1[i-1]==word2[j-1] |
初始化状态
对于 dp[i][0],相当于 word2 为空字符串,将 word1 转换为空字符串需要删除 i 个字符,即 dp[i][0]=i
对于 dp[0][j],相当于 word1 为空字符串,将 word2 转换为空字符串需要删除 j 个字符,即 dp[0][j]=j
代码
1 | function minDistance(word1: string, word2: string): number { |
两个字符串的删除操作
本题可以说是编辑距离的一个简化版本,对于两个字符串的操作仅限于删除字符,求最终的删除距离。
状态定义
和编辑距离一样,我们定义 dp[i][j] 为 word1 中以 i-1 为结尾的子串word1[:i-1]和 word2 中以 j-1 为结尾的子串word2[:j-1]要达到相等所需要删除的最小操作数。
我们定义 dp[i][j] 为 word1 中以 i-1 为结尾的子串word1[:i-1]和 word2 中以 j-1 为结尾的子串word2[:j-1]要达到相等所需要删除的最小操作数。
那么,对于word1[i-1]和word2[j-1]而言有两种情况:
word1[i-1]==word2[j-1],此时说明遇到相同元素,则说明word1[i-1]和word2[j-1]都不用删除,最小操作数dp[i][j]直接等于dp[i-1][j-1],即直接在子串word1[:i-2]和word2[:j-2]中操作即可word1[i-1]!=word2[j-1],此时有三种情况:- 两次删除操作,删除
word1[i-1]和word2[j-1],此时dp[i][j]=dp[i-1][j-1]+2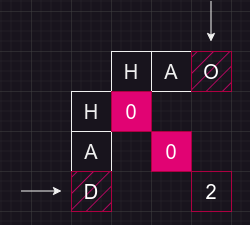
- 一次删除操作,删除
word1[i-1],此时dp[i][j]=dp[i-1][j]+1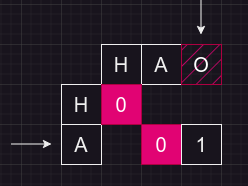
- 一次删除操作,删除
word2[j-1],此时dp[i][j]=dp[i][j-1]+1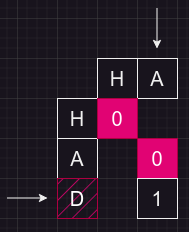
- 三种情况中取最小的一个,即
dp[i][j]=min(dp[i-1][j-1]+2, dp[i][j]=dp[i-1][j]+1, dp[i][j]=dp[i][j-1]+1)
- 两次删除操作,删除
最终的状态转移公式:
1 | |- dp[i-1][j-1],word1[i-1]==word2[j-1] |
初始化状态
对于dp[i][0]表示 word2 为空串,字符串 word1 要删除 i 个字符才能与空字符串相等,因此dp[i][0]要初始化成 i。
对于dp[0][j]表示 word1 为空串,字符串 word2 要删除 j 个字符才能与空字符串相等,因此dp[0][j]要初始化成 j。
代码实现
1 | function minDistance(word1: string, word2: string): number { |
不同的子序列
本题要求 s 中有多少子序列包含 t,其实就相当于是对 s 做多少删除操作能够得到 t,也算是编辑距离,或者说上面两个字符串的删除题目的简化版。
状态定义
我们定义 dp[i][j] 为字符串 s 中以 i-1 为结尾的子串s[:i-1]中出现以 j-1 为结尾的 t[:j-1]的个数,那么最终要求的结果便是 dp[s.length][t.length]
我们定义
s[:i-1]表示以 i-1 为结尾的 s 的子串,t[:j-1]表示以 j-1 为结尾的 t 的子串
对于 s[i-1] 和 t[j-1] 有两种情况:
s[i-1]==t[j-1]- 当两者相等时,
dp[i][j]有两部分组成: - 一部分是直接用
s[:i-1]来匹配t[:j-1],这种情况下由于s[i-1]==t[j-1],因此个数等于dp[i-1][j-1] - 一部分是
s[:i-1]子串删除字符s[i-1]来匹配t[:j-1],这种情况下,个数为dp[i-1][j]为什么删除
s[i-1]而不删除t[j-1],因为我们要做的是对 s 做删除操作得到 t
- 当两者相等时,
s[i-1]!=t[j-1]- 当两者不相等时,
dp[i][j]只有一部分组成,相当于s[:i-1]直接删除s[i-1]来匹配,个数为dp[i-1][j]
- 当两者不相等时,
所以最终的状态转移公式为:
1 | |--- dp[i-1][j-1]+dp[i-1][j], s[i-1]==t[j-1] |
初始化状态
我们将 dp[i][0] 都初始化为 1,将 dp[0][j] 都初始化为 0。
对于 dp[i][0] 表示的是 s 的任意子串如何操作得到空串 t,那肯定是删除全部的字符得到空串,只有这一种方法,因此初始化为 1。
对于 dp[0][j] 表示空串 s 如何做删除操作得到长度为 j 的字符串 t,这种情况无论如何也不能通过删除操作得到,因此初始化为 0。
注意两者有一个交集dp[0][0],设置为 1。因为空串可以不做任何操作就可以得到空串。
代码实现
1 | function numDistinct(s: string, t: string): number { |
最长公共子序列
最长公共子序列,也可以算是编辑距离延伸出来的一道题。要求两个字符串的最长公共子序列,可以认为是对两个字符串进行删除不同元素操作,然后留下最长的公共子序列。
定义状态
我们定义状态 dp[i][j] 表示 text1 中以 i-1 为结尾的子串 text1[:i-1]与 text2 中以 j-1 为结尾的子串 text2[:j-1]的最长公共子序列长度。
对于 text1[i-1] 和 text2[j-1] 比较,有两种情况:
text1[i-1]==text2[j-1],如果两者相同,相当于找到了相同元素,那么dp[i][j]=dp[i-1][j-1]+1text1[i-1]!=text2[j-1],两者不同,那么我们可以找 text1[:i-2]与 text2[:j-1]的最长公共子序列长度和 text[:i-1]与 text2[:j-2]的最长公共子序列的长度,取最大的。
因此,状态转移方程如下:
1 | |-- dp[i-1][j-1]+1, text1[i-1]==text2[j-1] |
初始化状态
我们初始化 dp[i][0] 和 dp[0][j] 都为 0,因为 dp[i][0]和 dp[0][j]可认为是空格与其他字符串的最长公共子序列长度,空格与任意字符串的最长公共子序列都是 0。
代码实现
1 | function longestCommonSubsequence(text1: string, text2: string): number { |
判断子序列
双指针
本题一般会使用双指针解决,而且双指针也是解决本题一种高效的算法。
1 | // 双指针 |
但除此之外,还可以用动态规划的思路来解决,而且与编辑距离还是有点关系。
动态规划
要判断 s 是否是 t 的子序列,相当于判断 s 和 t 的最长公共子序列长度是否等于 s 的长度,如果最长公共子序列长度等于 s 的长度,那么说明整个 s 便是 t 的一个子序列。这样就和上面的 【最长公共子序列】是一道题了。
具体的状态考定义和状态转移方程是一样的,可以参考上题,唯一不同点在于返回值,需要判断一下长度是否相等即可。
1 | function isSubsequence2(s: string, t: string): boolean { |
除了上面这几个和编辑距离相关的字符串的题目之外,其实还有一些数组的题目,其解题思路也和编辑距离类似。
数组也会有子序列,子数组的概念,所以这里一并把几个与数组相关的类似的题目整理一下。
最长重复子数组
本题和上面【最长公共子序列】类似,可以说是其一个变种题。
定义状态
本题要求两个数组的最长连续子数组,而子数组为一个数组的连续切片,即占据连续的位置。比如数组 [1,2,3,2,1], 其中 [1,2,3]是其一个子数组,而 [1,3,2] 不是其子数组,而只能算其子序列。
由于子数组占据连续的位置,因此我们定义状态 dp[i][j] 表示以 nums1[i-1] 为结尾的子数组和以 nums2[j-1] 为结尾的子数组的最长重复子数组长度。
那么整个题目的解便是 dp 的最大值。
对于 nums1[i] 和 nums2[j] 相比较,有两种情况:
nums1[i]==nums2[j]: 两者相等,说明遇到相同的元素,那么dp[i][j]=dp[i-1][j-1]+1nums1[i]!=nums2[j]: 两者不相登,那么以两者作为结尾的子数组必然不会相等,长度为 0,即dp[i][j]=0
最终的状态转移方程是:
1 | |- dp[i-1][j-1] + 1, nums1[i-1]==nums2[j-1] |
初始化状态
根据状态的定义,dp[i][j] 表示以 nums1[i-1] 为结尾的子数组和以 nums2[j-1] 为结尾的子数组的最长重复子数组长度,那么对于 dp[0][j] 和 dp[i][0] 而言,相当于是 nums1 为空和 nums2 为空的两种情况,所以默认都初始化先为 0。即 dp[0][j]=0, dp[i][0]=0。
代码实现
1 | function findLength(nums1: number[], nums2: number[]): number { |